| > Forums > NAVIGATION > Calcul de marée | |||||||||||||||||||||||||||||||||||||||||
| Messages | |||||||||||||||||||||||||||||||||||||||||
Sujet : Calcul de marée |
|||||||||||||||||||||||||||||||||||||||||
| .:pmephisto:. Nb post : 33 Depuis : 17/08/10 |
Ecrit le : 06/09/10 à 17:02:30
Calcul de maréeUn article de Wikipédia, l'encyclopédie libre. Le calcul de marée est la méthode utilisée en navigation maritime pour estimer la hauteur d'eau, dans un lieu et à un instant donné, en prenant en compte l'influence de la marée. Les marées sont le résultat de l'attraction de la lune et du soleil sur les mers et océans. Cette attraction varie avec le déplacement relatif du soleil et de la lune par rapport à la terre. Elle est au plus fort quand le soleil et la lune sont en conjonction ou en opposition cest-à-dire au moment de la pleine lune et de la nouvelle lune. Du fait de l'inertie des océans, il s'écoule, selon les lieux, entre 1 et 5 jours avant que la variation de l'attraction fasse effet sur la force de la marée. Ainsi sur les côtes françaises, les marées les plus fortes (vives eaux) ont lieu 36 heures après les syzygies : conjonctions ou oppositions de la lune et du soleil. Un peu de théorieLe potentiel générateurLa présence de la Lune et du Soleil, et leur mouvement, sont à l'origine de forces de gravitation qui génèrent la marée. La force génératrice de la marée dérive d'un potentiel que nous allons décrire ici. La distance de la terre à la lune est d'environ 380 000 km alors que le rayon de la terre est d'environ 6 400 km. La terre peut donc être représentée par un point matériel placé au centre de notre globe et affecté de toute la masse terrestre. Cependant l'attraction que subit une particule en un point quelconque du globe diffère en amplitude et en phase. Notons Π, le potentiel dont dérive la force génératrice de la marée. Dans un repère géocentrique on écrit ce potentiel appliqué à un point P de la surface du globe, affecté des coordonnées (a,λ,φ) sous la forme :
avec :
On peut exprimer d en fonction de a, RLune et ψ par la relation issue du théorème d'Al Kashi (voir figure représentation Terre - Lune) :
si on exprime 1/d, l'équation précédente (eq 1.2) devient :
La lune et le soleil sont les seuls astres dont l'influence est notable dans la génération des marées, l'un en raison de sa proximité, l'autre en raison de sa masse. Le terme a / RLune vaut environ 1 / 60 pour la lune et 1 / 2,5.104 pour le soleil. On peut donc estimer que :  Il devient donc possible, avec cette supposition de décomposer (eq 1.3) sous la forme d'une somme de polynômes de Legendre. 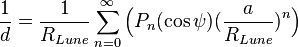 avec les polynômes de Legendre définis par : Si on se limite à l'ordre 2 qui représente déjà 98% du signal[1], on peut écrire le potentiel (eq 1.1) sous la forme :
On donne les coordonnées (RLune,λLune,φLune) à l'astre et les coordonnées (RP,λP,φP) au point du globe P, on peut donc exprimer cos(ψ) sous la forme : 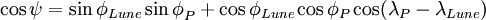 L'équation (eq 1.4) devient alors :   ![+\cos (2\phi_{Lune})\cos (2\phi_{P}) \cos2(\lambda_{P}-\lambda_{Lune}) \Big]](http://upload.wikimedia.org/math/c/7/3/c73b3ed2bb54daeed60d3af6a9af61dd.png) (eq : 1.5) (eq : 1.5)Si on détaille chacun des trois termes de l'équation (eq 1.5), et que l'on ne considère que le mouvement de rotation de la Terre en un jour, nous pouvons obtenir les termes de génération des premières ondes de marée. En effet :
Nous ne développerons pas davantage ici le potentiel en fonction de tous les mouvements orbitaux des deux astres perturbateurs. Nous ne citerons que les travaux de Darwin :
Ce sont Darwin et Doodson qui ont nommé les termes du développement du potentiel, ces noms sont toujours utilisés pour nommer les ondes. Les noms correspondent à un assemblage d'informations, ainsi M2 vient de M (Moon) un terme lunaire et 2 un terme semi-diurne, il en est de même pour l'onde solaire S2. L'onde de maréeL'attraction de la lune et du soleil crée une onde de marée qui, en se propageant, crée le phénomène de marée. La vitesse de propagation est élevée dans les eaux profondes (400 nuds en Atlantique), beaucoup plus faible dans les eaux peu profondes (30 nuds en Manche). Cette vitesse détermine le décalage des horaires de pleine mer en différents lieux. La forme de la maréeL'ampleur et la périodicité de la marée dépendent du lieu : ils sont déterminés par de nombreux facteurs dont la taille du bassin maritime, sa profondeur, le profil des fonds marins, l'existence de bras de mer, la latitude, etc. Dans certaines mers, comme la Méditerranée, tous ces facteurs sont à l'origine d'une marée tellement faible qu'elle peut être négligée. Ailleurs les marées peuvent atteindre plus de 10 mètres de marnage. Selon le lieu, du fait des caractéristiques ci-dessus, on distingue des marées de 3 types :
La prédiction des maréesLa marée peut être calculée longtemps à l'avance puisqu'elle dépend uniquement de caractéristiques constantes :
Par des observations répétées, les services chargés de prédire les marées (en France, le SHOM), ont mis au point des modèles permettant de calculer à l'avance les horaires et les hauteurs des marées futures. Les caractéristiques d'une maréeUne marée, en un lieu et à une date et une heure données, est définie par :
Effectuer le calcul d'une hauteur d'eau dans les eaux de l'Atlantique et de la Manche en FranceNB: Les calculs de hauteur d'eau, effectués en particulier avec la méthode des douzième listée ci dessous, ne sont pas précis. Il est conseillé d'utiliser les courbes types de chaque port principal (données dans l'ouvrage du SHOM)[2]. De plus, quelle que soit la méthode utilisée, le navigateur devrait prendre une marge de sécurité (pied de pilote) qu'il fixera en fonction de son expérience personnelle. Les marées en FranceLes marées en France métropolitaine sont de type semi-diurne, ce qui signifie qu'il y a de manière générale deux pleines mers et deux basses mers en 24 heures (en réalité, 24h50mn en moyenne). Par exemple, le 4 février 2006, les horaires des marées à Saint-Malo sont les suivants :
Les coefficients de ces marées sont respectivement de 77 et 69. Le coefficient de maréeEn France, l'ampleur de la marée par rapport à sa valeur moyenne est indiquée par le coefficient de la marée qui prend une valeur comprise entre 20 et 120. La valeur 100 est associée à une amplitude d'une marée fixée arbitrairement par le SHOM.
Remarque : le coefficient de marée est identique dans un bassin donné à une date donnée pour une marée donnée (par exemple, les côtes de la Manche et de l'Atlantique) car elles sont touchées par la même onde de marée alors que le marnage varie car il dépend de la configuration de la zone côtière. Le référentiel utilisé pour les hauteurs de maréeLes hauteurs de marée sont indiquées en France par rapport au zéro hydrographique qui est voisin du niveau le plus bas que peut atteindre théoriquement la mer, soit la hauteur d'eau à la basse mer d'une marée de coefficient 120 (coefficient de marée le plus élevé). La règle des douzièmes Souvent, la variation de la hauteur d'eau est lente au début de la marée, plus forte à mi marée et se réduit en fin de marée (marée dite sinusoïdale). On peut approcher cette évolution sinusoïdale en appliquant la règle des douzièmes, on utilise alors une ligne brisée qui se rapproche de la courbe sinusoïdale. Si on divise en 6 unités de temps la période qui s'écoule entre basse mer et pleine mer, la variation relative du niveau des eaux est approximativement de 1/12 durant la première unité de temps, 2/12 la deuxième unité de temps, puis 3/12, 3/12, 2/12, 1/12 (soit 1/12, 3/12, 6/12, 9/12, 11/12, 12/12). Le sixième de marée est appelé "heure de marée" ou "heure-marée". Appliqué à la première marée montante du 4 février à Saint-Malo, on obtient :
soit une marée de 323 minutes; l'heure de marée est de (323/6)= 54 minutes
la différence (marnage) est de 9,05 mètre (11,3-2,25) ⇒ 1/12 = 75,42 cm Ce qui donne le tableau suivant des hauteurs d'eau :
La méthode graphique du demi-cercleSur le même principe que la méthode des douzièmes qui est une approximation d'une courbe sinusoïdale, on peut graphiquement trouver une hauteur d'eau en fonction de l' "heure de marée" et vice-versa en dessinant un demi-cercle. Soit un demi-cercle :
 La projection sur le diamètre (le cosinus) correspond à la hauteur d'eau.
Les correctionsLes horaires, les coefficients et les hauteurs d'eau des marées sont fournis dans l'Annuaire des Marées des guides nautiques pour les ports principaux. Pour des ports dit rattachés comme Cancale, les heures et les hauteurs des marées se déduisent des caractéristiques de la marée du port principal dont ils sont proches (Saint-Malo) en appliquant des corrections (par exemple +5 minutes et +0,75 cm); ces données sont indiquées pour les marées de vives eaux et de mortes eaux (on interpole pour les marées moyennes). Le calculPour calculer la profondeur (P), la démarche est donc la suivante :
 Incidence des conditions météorologiquesCertains phénomènes atmosphériques peuvent avoir une influence sur la hauteur d'eau : Les données sont valables pour une pression atmosphérique moyenne (1013 hPa), les hauteurs doivent être corrigées de 10 cm pour 10 hPa de variation par rapport à la pression moyenne. Exemples:
Quelques exemples de marée en FranceEn France, le marnage est très faible en Méditerranée. Il est maximal dans la région de Saint-Malo / Granville et va décroissant en descendant le long de la côte atlantique. En voici quelques exemples : Vives Eaux Marée : coefficient 116 (1er mars 2006). 116 est le plus gros coefficient de marée de l'année 2006.
Mortes Eaux : coefficient 28. 28 est le plus petit coefficient de marée de l'année 2006.
Le courant de maréeArticle détaillé : Courant de marée. Le déplacement des eaux par la marée génère le long des côtes des courants dont la force dépend du moment de la marée, de l'ampleur locale de la marée et de la configuration des lieux. En France les courants de marée les plus puissants sont rencontrés dans le Raz Blanchard où leur vitesse peut atteindre 12 nuds en vives eaux. Notes
Annuaire Marées 07 Fr T1 |
||||||||||||||||||||||||||||||||||||||||
| 1 | |||||||||||||||||||||||||||||||||||||||||

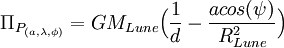 (eq : 1.1)
(eq : 1.1) (eq : 1.2)
(eq : 1.2) (eq : 1.3)
(eq : 1.3)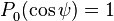

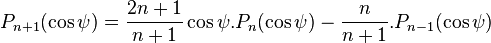
 (eq : 1.4)
(eq : 1.4) effectue deux périodes lors d'une rotation de l'angle (λP − λLune) de 2π (rotation de la terre en 1 jour), il décrit donc une fonction semi-diurne.
effectue deux périodes lors d'une rotation de l'angle (λP − λLune) de 2π (rotation de la terre en 1 jour), il décrit donc une fonction semi-diurne. 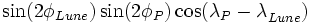 n'effectue qu'une période lors d'une rotation, il décrit donc une formule diurne.
n'effectue qu'une période lors d'une rotation, il décrit donc une formule diurne. 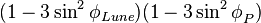 ne dépend pas de la longitude mais uniquement de la latitude de l'astre et du point de mesure, ce terme varie en fonction du mouvement de déclinaison de l'astre (période > > 24h), il décrit donc une fonction longue période.
ne dépend pas de la longitude mais uniquement de la latitude de l'astre et du point de mesure, ce terme varie en fonction du mouvement de déclinaison de l'astre (période > > 24h), il décrit donc une fonction longue période. 